A neuron performs a two-step process:
- Linear Transformation: It calculates a weighted sum of its inputs and adds the bias term. Mathematically, this can be represented as:
Where $w_i$ are the weights, and $x_i$ are the inputs.
- Activation: The result from the above step is then passed through an activation function, producing the neuron’s output. Common activation functions include the sigmoid, hyperbolic tangent (tanh), and Rectified Linear Unit (ReLU). Graphs of these are below. The activation function to use is one hyperparameter. Empirically, the ReLU has become popular because it works well in many situations and is computationally quick to calculate.
Common Activation Functions
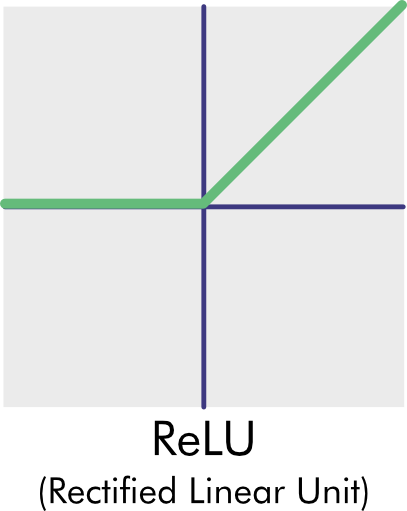
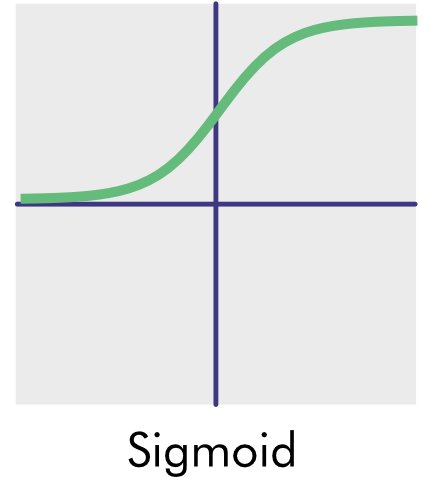
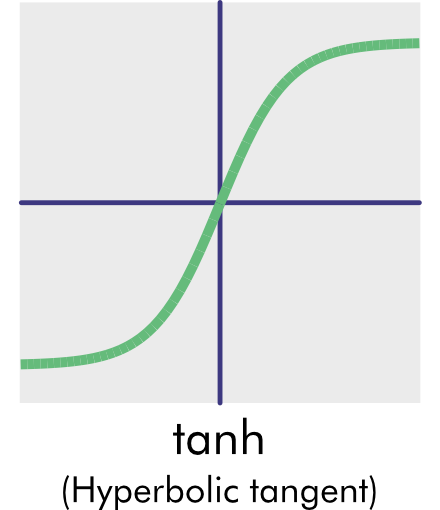
In these graphs, the neuron raw output is on the x-axis, and the output, as transformed by the activation function, is on the y-axis. The y-axis crosses the x-axis at the origin (0,0).
Functions, ACTIVATE!
As mentioned above, activation functions introduce non-linearity to the model, allowing neural networks to capture complex relationships and patterns in the data. Without them, no matter how deep the network, it would behave like a linear model, limiting its predictive power. As an analogy, imagine building a complex structure out of blocks. If you only use straight pieces, you’re limited in what shapes you can create. But introduce some curved or angled pieces (akin to activation functions), and suddenly, you can build intricate and varied designs. Here are some examples of some of the more popular activation functions.
- Step Function: Our first activation function is the simple step function. When its input is less than or equal to zero, the perceptron outputs 0. If the input becomes positive – even by a tiny amount – the perceptron outputs a 1. But this sudden and extreme transition is not ideal for training. Essentially, the neuron has no finesse – it’s either yelling or silent. Step functions only work for modeling single, straight lines like those in binary classifiers and are rarely used in deep learning.
- ReLU (Rectified Linear Unit) Function: The ReLU (rectified linear unit) function outputs 0 for all negative inputs; otherwise, the output is the input. The ReLU activation function has recently become quite popular because it’s simple and trains exceptionally well. The angles it outputs allow it to model linear functions and make excellent approximations of curves if there is enough capacity in the network.
- Sigmoid (or Logistic) Function: The sigmoid function – also known as the logistic function – returns a 0 value for extremely negative inputs and a value of 1 for extremely positive inputs. This function is called sigmoid because it resembles the curve of an S shape. Because of its binary output, this function works well for binary classifiers that are separated by a curved line rather than a straight one.
- tanh Function: The output of the tanh is a hyperbolic tangent and looks like the sigmoid function. It has that same S-shape. But there are differences. For example, the TANH function returns a value of −1 for extremely negative inputs.



