Finding the ideal hyperparameter settings is part art, part science. Here are common methods with images taken from Figure 1 of the paper “Random Search for Hyper-Parameter Optimization” (Bergstra and Bengio, 2012, Journal of Machine Learning Research 13):
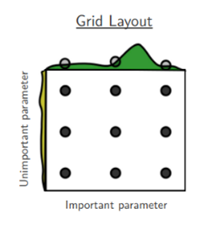
Grid Search
Creates a grid of pre-defined hyperparameter values. The model is trained and evaluated for every combination on that grid.
Pro
- Useful when you have fewer hyperparameters and want to test their effects systematically.
Cons
- Computationally expensive, especially as the number of hyperparameters and their ranges grow.
- Can miss sets of parameters not included in the grid search.
- Can waste search effort on different values of unimportant parameters.
When to Use Grid Search:
- Limited Hyperparameters: You have only a few crucial hyperparameters you want to tune.
- Computational Resources: You can access the compute resources for a comprehensive search.
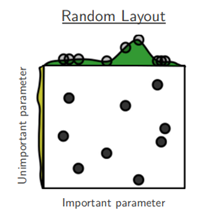
Random Search
Randomly samples hyperparameter combinations from a defined distribution. Not every point in the space is tested.
Pros
- Surprisingly efficient! Often finds better settings faster than grid search.
- Better chance of exploring diverse areas of the hyperparameter space.
- Scales better with a larger number of hyperparameters.
Cons
- No guarantee of finding the absolute best configuration.
- Difficult to visualize results compared to the structured output of grid search.
When to Use Random Search:
- Best for most cases!
- Lots of Hyperparameters: When tuning more than a few hyperparameters.
- Speed Matters: Useful for when you need to find reasonably good settings quickly.
In practice, random search is typically the preferred starting point due to its efficiency. If you then need to refine the search further, you can use a grid search around the best-performing areas found from the random search. Hybrid approaches are also possible, where some hyperparameters are grid searched while others are random searched.
Tools to the Rescue
Here are two examples of tools for searching for optimized hyperparameters:
- TensorBoard’s HParams: Integrated into TensorFlow. Helps compare different experimental runs using interactive visualizations. Simple interface for defining your hyperparameter search space and tracking results.
- Optuna: A dedicated hyperparameter optimization framework. Offers a wider array of search algorithms (grid, random, and more advanced techniques). Can intelligently prune unpromising trials early. Rich visualization tools.
- Ray Tune: Designed for distributed execution across multiple machines. Wide range of search and scheduling algorithms. Fault-tolerance mechanisms and good integration with popular ML libraries.
We recommend starting with TensorBoard’s HParams if your tuning needs are relatively straightforward and you’re working within the TensorFlow ecosystem. For more complex searches, advanced features like pruning, or distributed tuning needs, consider the extra power provided by Optuna or Ray Tune.
Return to Module 3 or Continue to Developing Hyperparameter Intuition for Computer Vision



